12-20 22:51:13 浏览次数:159次 栏目:高一数学试题

9.BC是Rt△ABC的斜边,AP⊥平面ABC,PD⊥BC于点D,则图中共有直角三角形的个数是( )
A. 8 B. 7 C. 6 D. 5
10.圆C:x2+y2+2x![]() +4y-3=0上到直线
+4y-3=0上到直线 :x+y+1=0的距离为
:x+y+1=0的距离为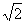 的点共有( )
的点共有( )
A.1个 B.2个 C.3个 D.4个
11.求经过点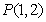 的直线,且使
的直线,且使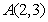 ,
,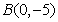 到它的距离相等的直线方程.( )
到它的距离相等的直线方程.( )
A.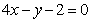 B.
B. 
C. 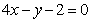 ,或
,或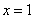 D.
D. 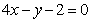 ,或
,或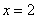
12.当点P在圆x2+y2=1上变动时,它与定点Q(3,0)相连,线段PQ的中点M的轨迹方程是( )
A. (x+3)2+y2=4 B. (x-3)2+y2=1 C. (2x-3)2+4y2=1 D. (2x+3)2+4y2=1
第Ⅱ卷
二、填空题(本大题共4小题,每小题5分,共20分.把正确答案填在答题卡的横线上,填在试卷上的答案无效)
13. 经过圆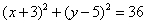 的圆心,并且与直线
的圆心,并且与直线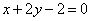 垂直的直线方程为_____.
垂直的直线方程为_____.
14. 以A(4,3,1),B(7,1,2),C(5,2,3)为顶点的三角形形状为 .
15.已知实数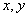 满足
满足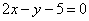 ,则
,则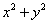 的最小值为________.
的最小值为________.
16.半径为R的球放在墙角,同时与两墙面和地面相切,那么球心到墙角顶点的距离为 .
www.170xue.com
三、解答题:(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算 步骤.)
步骤.)
17.(本小题满分10分)
过点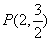 的直线
的直线 与
与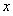 轴的正半轴、
轴的正半轴、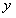 轴的正半轴分别交于点
轴的正半轴分别交于点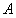 、
、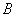 ,
,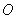 为坐标原点,
为坐标原点,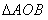 的面积等于6,求直线
的面积等于6,求直线 的方程.
的方程.
18.(本小题满分12分)
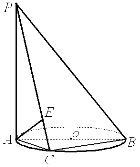
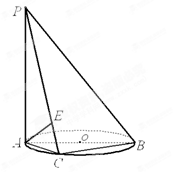 如图,
如图,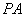 垂直于⊙
垂直于⊙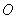 所在的平面,
所在的平面,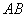 是⊙
是⊙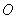 的直径,
的直径,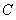 是⊙
是⊙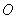 上一点,过点
上一点,过点 作
作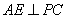 ,垂足为
,垂足为 .
.
求证: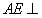 平面
平面
19.(本小题满分12分)
如图,在正方体ABCD-A1B
(1)求证:EF ∥平面CB
(2)求证:平面CAA1

20.(本小题满分12分)
已知圆C: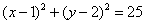 ,直线L:
,直线L: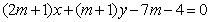
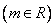
(1)证明:无论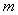 取什么实数,L与圆恒交于两点;
取什么实数,L与圆恒交于两点;
(2)求直线被圆C截得的弦 长最小时直线L的斜截式方程.
长最小时直线L的斜截式方程.
21.(本小题满分12分)
已知圆 与圆
与圆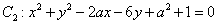 (其中
(其中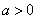 ) 相外切,且直线
) 相外切,且直线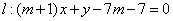 与圆
与圆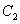 相切,求
相切,求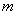 的值.
的值. 
22.(本小题满分12分)
已知动点M到点A(2,0)的距离是它到点B(8,0)的距离的一半,求:
(1)动点M的轨迹方程;
(2)若N为线段AM的中点,试求点N的轨迹.
参考答案:

 18.证明:因为
18.证明:因为 平面
平面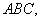 所以
所以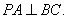
又因为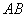 是⊙
是⊙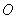 的直径,
的直径,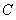 是⊙
是⊙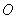 上一点,
上一点,
所以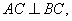 所以
所以 平面
平面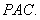
而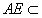 平面
平面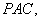 所以
所以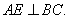
又因为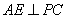 ,所以
,所以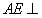 平面
平面
 19.证明:(1)连结BD.
19.证明:(1)连结BD.
在正方体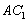 中,对角线
中,对角线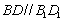 .
.
又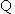 E、F为棱AD、AB的中点,
E、F为棱AD、AB的中点,
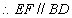 .
. 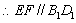 .
.
又B1D1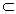 平面
平面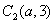 ,
,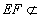 平面
平面 ,
,
 EF∥平面CB1D1.
EF∥平面CB1D1.
(2)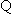 在正方体
在正方体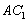 中,AA1⊥平面A1B
中,AA1⊥平面A1B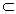 平面A1B
平面A1B
 AA1⊥B
AA1⊥B
又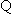 在正方形A1B
在正方形A1B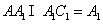
 B
B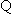 B
B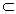 平面CB
平面CB
 平面CAA1
平面CAA1

21.解:由已知,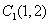 ,圆
,圆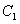 的半径
的半径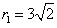 ;
;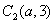 ,圆
,圆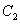 的半径
的半径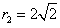 .
.
因为圆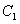 与圆
与圆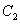 相外切,所以
相外切,所以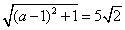 .
.
整理,得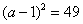 . 又因为
. 又因为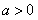 ,所以
,所以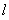 .
.
因为直线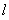 与圆
与圆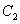 相切,所以
相切,所以 ,
,
即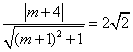 .
.
两边平方后, 整理得
整理得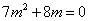 ,所以
,所以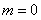 或
或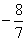 .
.
22.解:(1)设动点M(x,y)为轨迹上任意一点,则点M的轨迹就是 集合P={M||MA|=|MB|}.
集合P={M||MA|=|MB|}.
由两点间距离公式,点M适合的条件可表示为
√[(x-2)2+y2]=1/2√[(x-8)2+y2]
平方后再整理,得x2+y2=16.可以验证,这就是动点M的轨迹方程.
(2)设动点N的坐标为(x,y),M的坐标是(x1,y1).
由于A(2,0),且N为线段AM的中点,
所以x=(2+x1)/2,y=(0+y1)/2.
所以有x1=2x-2,y1=2y.①
由(1)知,M是圆x2+y2=16上的点,
所以M的坐标(x1,y1)满足x12+y12=16.②
将①代入②整理,得(x-1)2+y2=4.所以N的轨迹是以(1,0)为圆心,2为半径的圆.
,高一上册数学期末试卷及答案(理科)tag: 数学 高一数学试题,高一数学试题大全,高一数学学习方法,高中学习 - 高一学习 - 高一数学 - 高一数学试题
相关分类
高一数学试题 推荐